Klein geometry

A Klein geometry is a pair $(G,H)$ where $G$ is a Lie group and $H$ is a closed Lie subgroup of $G$ such that the coset space

is connected. We can call $X$ the "underlying geometrical space" (non-standard terminology). (If $X$ were not connected it would be say that we have a Klein geometry non geometrically oriented. This has nothing to do with being an oriented manifold).

A Klein geometry is effective if the largest subgroup $K\subseteq H$ that is normal in $G$ is $\{id\}$. The idea is that in this case the action of $G$ on $X$ is effective, that is, $G$ can be injected in the bijections group of $X$.

Another important class of Klein geometries are the reductive Klein geometrys.

Observe that $G$ acts transitively on $X$ and $H$ is the isotropy group of a point $x\in X.$ This construction can therefore be reversed and say that a Klein geometry is a homogeneous space $(X,G)$, and $H$ appears as the isotropy group of certain $x_0 \in X$. The choice of $x_0$ is not important, because all the isotropy groups are conjugate.

This theorem shows that this reversed construction is fine even in the smooth manifolds category:

Theorem Let $G$ be a Lie group and $H$ be a closed Lie subgroup of $G$. Then there exists a unique smooth structure on the quotient space $G/H$, denoted by $N$, such that $N$ becomes a smooth manifold and the natural action of $G$ on $N$ is smooth. Further, suppose $M$ is a smooth manifold on which $G$ acts smoothly and transitively. Let $x_0 \in M$ and $G_{x_0}$ denote the stability subgroup at $x_0$. Then the map

is a smooth diffeomorphism from $G/G_{x_0}$ onto $M$.$\blacksquare$

Proof Theorem 2.9.4 in V. S Varadarajan. Lie Groups, Lie Algebras, and Their Representations. 1st ed. Springer,1984$\blacksquare$

What this theorem says is that if there is a Lie group and a Lie subgroup, their quotient is a smooth manifold. On the other hand, it also says that if there is a Lie group that acts smoothly and transitively on a smooth manifold, then the stabilizer of any point (which is closed) can be quoted with the Lie group which then becomes the manifold in question.

Observation: if the group is not closed the action is not proper and the quotient is not a manifold. See example in @sharpe2000differential page 146.

Examples:

1. The pair $(E(2), O(2))$, that is the same as the homogeneous space $(\mathbb{R}^2,E(2)).$

2. Given a pseudo-Riemannian manifold $(M,g)$, if we denote $G=Isom(M,g)$ the group of its isometries and take $H=Stab_G(x)$ for certain $x\in M$ the pair $(G,H)$ is a Klein geometry (I think). And also I think that we can recover the metric $g$ from the pair $(G,H)$(????)

Relation with Cartan geometry

A Klein geometry $(G,H)$ gives rise to a principal $H$-bundle

with standard fibre $H.$ See Theorem 2.4 in @sharpe2000differential together with the fact that the right action of $H$ on $G$ is proper action and free action.

The Maurer-Cartan form of $G$ as a Lie group and the Maurer-Cartan form as principal bundle of $H$ are related. That is to say, since $G$ is a Lie group itself, then we can think of the "global" Maurer-Cartan form $\theta$. And since it is a principal bundle we can think of the "fibrewise" Maurer-Cartan form $\theta^P$ (the $P$ stands for "principal bundle"). For any $V\in T_pP$ we have $\theta(V)\in \mathfrak{g}$ but if $V\in V_pP$ then also

Proof

Suppose $\theta(V)=v$, then $V=d(L_p)_e(v)$ by definition. But since $v=\frac{d}{dt}|_{t=0} e^{tv}$, by definition of the exponential map, then

and so $\theta^P(V)=v$. But we need to show that $v\in \mathfrak{h}$ in order to apply $i_p$. I think that this must be easily deduced from $i_p=d(L_p)_e|_{\mathfrak{h}}$... $\blacksquare$

In this sense, the Maurer-Cartan form of $G$ is a Cartan connection and therefore the Klein geometry $(G,H)$ gives rise to a Cartan geometry.

The structural equation of the Maurer-Cartan form is satisfied, so the curvature of this Cartan geometry is 0. That is, Klein geometries are flat Cartan geometries.

Personal approach

Given a Klein geometry or homogeneous space $(X,G)\equiv (G,H)$ with $H=Stab_G(x)$, we can construct others. For example, consider a subset $S\subseteq X$, and the stabilizer $\widetilde{H}=Stab_G (S)$, which I think is closed. Then $(G,\widetilde{H})$ is a new Klein geometry with underlying geometrical space

being $gS=\{gx:x\in S\}$. So we have the homogeneous space $(\widetilde{X},G).$ The points of this space are "copies" of the subset $S$ under the transformations given by $G$.

Observe that there is a bijection between $\widetilde{X}$ and $G/\widetilde{H}$, given trivially by

For example, consider $(\mathbb{R}^2,E(2)^+)$, being $E(2)^+$ the direct motions, for simplicity. We can consider $S$ an equilateral triangle with side 2 units. Then we can think that we are studying a space $\widetilde{X}$ whose points are the different equilateral triangles with side 2 units that you can put in $\mathbb{R}^2$. This corresponds to shrink $H=SO(2)$ to $\widetilde{H}=\langle r_{\pi/3}\rangle$ . The points in space $\widetilde{X}$ are not "so rounded" as those ones in $X$, since now they are sensible to some rotations.

On the other hand, If we shrink $H$ to $\widetilde{H}=\{id\}$ then we obtain $\widetilde{X}$ being the whole $E(2)^+$ but no natural choice of identity $e$, that is, a $E(2)^+$-torsor. The points of $X$ have became the most sensitive posible. It is as if we stick a rotation sensor to every point in the plane, so no motion in $SO(2)$ leaves them invariant.

On the contrary, if we extend $H$ instead of shrink it, we obtain less points. An extreme example: suppose we take $\widetilde{H}=G$, then $\widetilde{X}$ has only one element, the whole $X$.

So given a group $G$ (which Klein called _principal group_) that we can think as acting over a $G$-torsor $\widetilde{G},$ we have that every subgroup $K$ of $G$ is associated with a "basic object of study", a "feature", and a space that is the collection of all these "features" that appear by applying elements of $G$ to the basic "feature" (see [Wise 2009] page 7).

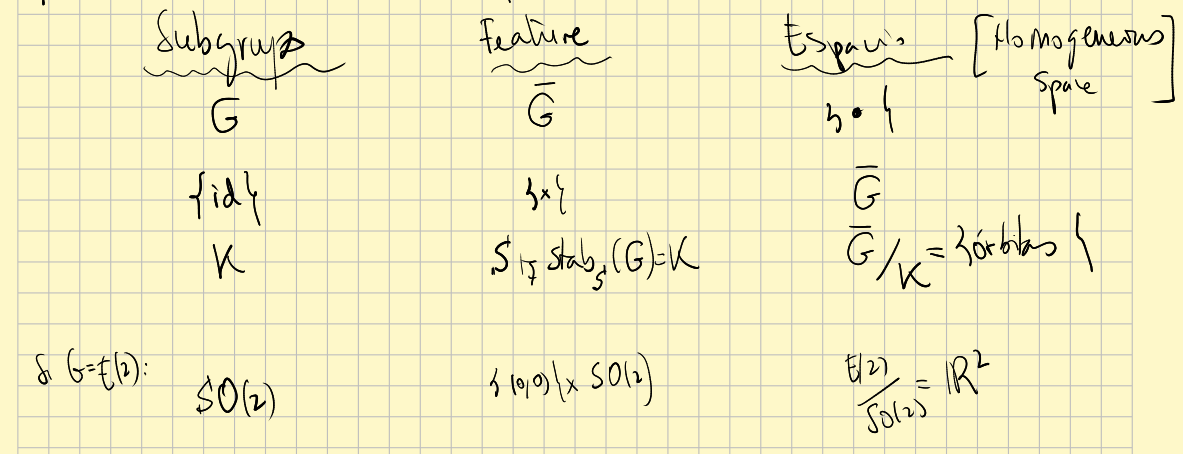
Another approach

The group $G$ establishes what kind of transformations do we start with (continuous, smooth, rigid,...?). The torsor $\widetilde{G}$ is the bigger _geometrical space_ in relation with $G$ (I think that in a bigger space the action wouldn't be transitive). And by fixing subgroups $K$ of $G$ we are creating smaller geometrical spaces, the space of $K$-orbits, that can be more interesting. For example, the group of direct rigid motions $E(2)^+$, when we consider the subgroup of rotations, gives rise to the usual euclidean plane. It is like if $\widetilde{G}$ are the different states of a "being", and when we deactivate some "senses" of that "being" appear smaller spaces.

This can be thought in the following way. Consider your smartphone but in a flat 2-dimensional world. Thanks to the GPS and orientation sensor, there are lots of posible "states" for the phone: every position and every orientation is different for it. If we "disconnect" the orientation sensor in our phone, then the different states are only the positions, and this is equivalent to consider as a whole the entire orbit of a point rotated over itself. That is to say, taking $H=SO(2)$, the rotations around a base point $x\in \mathbb{R}^2$.

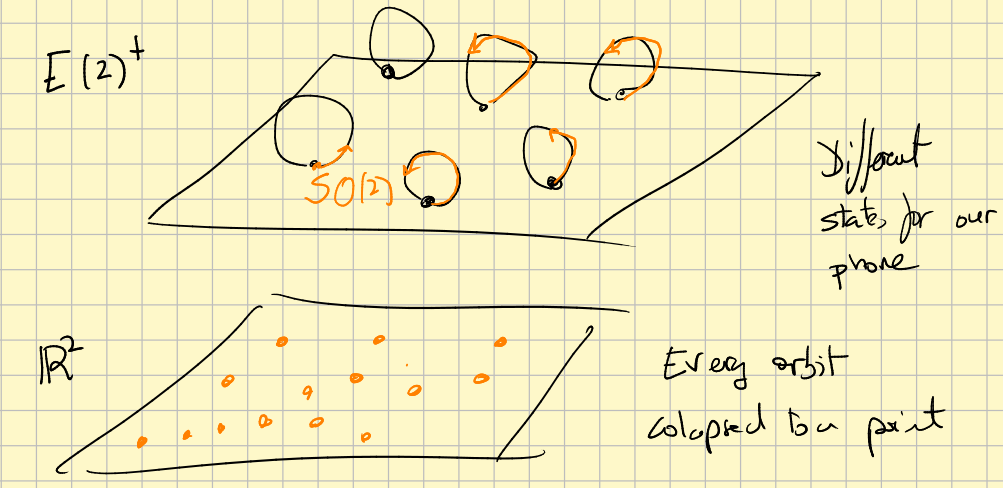
Observe that in the picture, if we fix a point $x\in \mathbb{R}^2$ we have an identification between points and cosets

being $g\in E(2)$ such that $g(x)=z$. Also, observe that given $h\in H=SO(2)$

and $ghg^{-1}\in gHg^{-1}$ is a "rotation" around the point $z=g(x)$. This way is easier to understand the picture.

Anyway, I think this is a special case, because the group has structure of semidirect product. When this happens, that is, when we have a Klein geometry $(G,H)$ in such a way that $G=N\rtimes H$, then the geometrical space $X=G/H$ is bijective to $N$, and $N$ acts on $X$ in a free and transitive way, that is, $X$ is a $N$-torsor. Proof:

In this case, $X$ is also a principal homogeneous space.

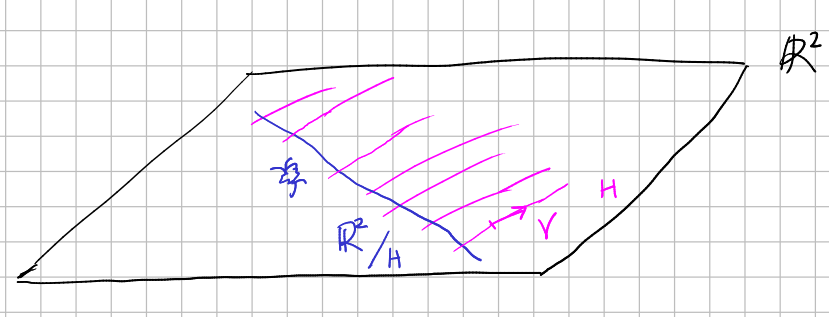
Another example: bugs living in a plane that can translate horizontally and vertically but which cannot rotate. For them, the relevant transformations are $(\mathbb{R}^2,+)$ and the geometrical space is, in principle, the whole $\mathbb{R}^2.$ Suppose that a kind of translations is less important than other, those performed in a certain direction $V$ (maybe because of the shape of their bodies they are easier to perform, or consume less energy to them...). Let $H$ be the subgroup of $(\mathbb{R}^2,+)$ given by this easier translations. Then their consciousness may be focus on a smaller space $\mathbb{R}^2/H$ (a real line) because is what is important for their survival.

Related idea: sweeping the porch of my little cabin. Since is much easier to sweep in one direction (is almost "free") my sub consciousness treat the porch like being 1-dimensional.

About recovering the geometric properties of $X$ from the pair $(G,H)$

See Where is the geometry in a Klein geometry?

I have found that the key is in the adjoint representation of $H$ over $\mathfrak{g}$. Because in this context we can look for invariant subspaces and I guess that "inside" is hidden the information for the geometry. I have seen a good explanation in *Parabolic Geometries*, by Andreas Cap and Jan Slovak, page 6, but I don't fully understand yet.

I have also found useful the foreword of *Differential geometry, Cartan's generalization of Klein Erlangen program*, by Sharpe and Chern; although I cannot see yet how the Maurer-Cartan form let us recover the metric.

Another clue: this question and answer in mathstackexchange.

________________________________________

________________________________________

________________________________________

Author of the notes: Antonio J. Pan-Collantes

antonio.pan@uca.es